• Regenerative braking
• Regen calculations

How much can be regenerated?

The following scenarios use math and physics to explain the significant benefits of regenerative braking.

In the physics chapter, we explain the details behind the calculations. However, it’s essential to understand that a moving object has kinetic energy that an EV can recover through regenerative braking. Similarly, a car in an elevated position has potential energy that can also be recovered.

Additionally, aerodynamic drag and rolling resistance work against the car’s movement.

The drivetrain is not without loss, meaning some energy is lost when converting energy from the battery to the car’s movement or vice versa. Typically, this efficiency is about 80-85% in an EV. For our calculations, we use 80%.

Scenario 1: Pikes Peak

Let’s take Pikes Peak as an example. This mountain is 14,110 ft (4,300 meters) high. If you drive down the first 18.6 miles, you descend 6,538 ft (1,993 meters).

For an Audi e-tron 55 weighing 2,900 kg, this descent equates to 15.74 kWh of potential energy.

The 18.6 miles (30 km) descent at a low speed, considering rolling resistance and a speed of 40 km/h, results in an energy consumption of 10.52 kWh/100 km.

For 30 km, this means 3.15 kWh in total. This energy will be subtracted from the potential energy.

Thus, 12.59 kWh can be regenerated. With 80% efficiency, this results in 10.07 kWh being returned to the battery.

In the video below, you can see a real-world test of this trip and the amount of energy regenerated.

Scenario 2: Full stop from 75 mph

In this scenario, the car is moving at 75 mph (120.7 km/h) and needs to make a full stop for a red light.

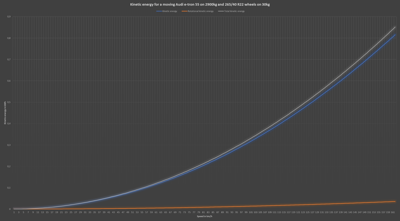
As shown in the graph below, stopping from 75 mph for a 2,900 kg Audi e-tron results in a total kinetic energy of 0.473 kWh.

With 80% drivetrain efficiency, the car can recover 0.38 kWh back to the battery.

A full trip of 100 km (62 miles) with 10 such stops would save 3.8 kWh compared to a car with only friction brakes.

This results in a consumption reduction of 3.8 kWh/100 km.

Scenario 3: Reduce speed from 30 mph to a full stop

This scenario represents typical city driving. When driving at 30 mph (48.28 km/h), the Audi e-tron has a total kinetic energy of 0.0756 kWh.

With 80% drivetrain efficiency, this saves 0.061 kWh back to the battery.

If you drive 100 km in city traffic and need to make 100 stops like this, you save 6.05 kWh of energy.

This regeneration reduces energy consumption by 6.05 kWh/100 km compared to a car with only friction brakes.

Scenario 4: Driving down from Saltfjellet mountain

This mountain is located in Northern Norway, and the main road from South to North passes over it (E6).

If we take this section of the road where it starts to go downhill, we see that the start is at 650 meters (2,132 feet) and it ends at 125 meters (410 feet) above sea level. With a distance of 16.4 km (10.2 miles), this gives a decline of 3.1%.

This results in potential energy of 4.147 kWh.

The speed limit is 80 km/h (49.7 mph), and based on standard consumption on a dry road, the car requires 2.49 kWh to roll this distance driven by the potential energy.

The rest can be regenerated, and with 80% efficiency, this gives 1.3 kWh back to the battery.

1.3 kWh should provide an additional range of 6.8 km at 80 km/h (49.7 mph).

Understanding the physics

Kinetic energy

A moving object has kinetic energy, which depends on the object’s mass and speed.

The formula is:

Where:

• KE = kinetic energy in Joules
• m = mass of the object in kilograms
• v = velocity of the object in meters per second

Additionally, 1 Joule is equivalent to 2.778·10⁻⁴ Wh.

In all calculations on this page, we use the Audi e-tron 55 with a weight of 2900 kg (car + driver). The table below shows the kinetic energy of this car at various speeds:

You can use this kinetic energy calculator for other speeds. See also the graph below.

Rotational kinetic energy

In addition to the car’s kinetic energy, the spinning wheels also contain rotational kinetic energy that can be regenerated.

The formula for rotational energy is:

Where:

• E = rotational kinetic energy in Joules
• I = moment of inertia in kg·m²
• ω = angular velocity in radians per second

The moment of inertia for a wheel can be calculated as:

[ I = M \times R^2 ]

For an Audi e-tron with wheel option 265/40 R22, and an estimated weight of 30 kg per wheel and a radius of 38.54 cm, the calculation is:

[ I = 30 \times 0.3854^2 = 4.4559948 ]

At 80 km/h, the wheel spins at 566.89 rpm, resulting in a kinetic energy of 8.724 Wh (0.008724 kWh) for four wheels.

Note: This calculation is an approximation since the formula assumes a uniform wheel shape from center to edge. However, it is sufficiently accurate for this context.

You can try the Rotational Kinetic Energy calculator for other calculations.

Gravitational/Potential energy

Potential energy exists when the car is at an elevated location compared to its destination.

The formula is:

Where:

• U = gravitational energy in Joules
• m = mass in kg
• g = gravitational field (9.8 m/s² on Earth’s surface)
• h = height in meters

For example, an Audi e-tron 55 weighing 2900 kg at 1000 meters (3280 feet) above sea level has a potential energy of 7.8998 kWh (28,492.85 Joules).

In areas with elevation, potential energy is the largest source of regenerated energy.

See the potential energy calculator.

Summary

The graph below shows the total kinetic energy and the two types of kinetic energy.

Understanding energy consumption

Before we provide examples of how much energy can be regenerated, we need to explain energy consumption, as it affects the results.

Consumption by aerodynamic drag

A moving car experiences air resistance that opposes its movement.

The formula for drag is:

Where:

• P = air density (1.225 kg/m³ at 15 °C)
• u = speed in meters per second
• A = frontal area of the car (2.65 m² for Audi e-tron)
• CD = drag coefficient (0.28 for Audi e-tron 55)

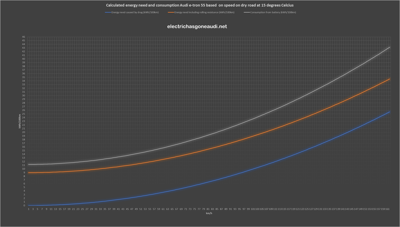
For example, at 80 km/h, the power required to overcome aerodynamic drag is 4.9 kW (6.23 kWh/100 km).

Note that the power needed to push an object through a fluid increases with the cube of the velocity. Thus, an Audi e-tron 55 traveling at 160 km/h requires 39.89 kW (24.94 kWh/100 km) to overcome drag.

Temperature affects air density. At -25 °C, the density is 1.4224 kg/m³, increasing consumption at 80 km/h to 7.23 kWh/100 km.

For all calculations in this article, we assume a temperature of 15 °C.

Rolling resistance

In addition to drag, rolling resistance from the wheels and other drivetrain components opposes movement.

Estimating rolling resistance is challenging, but by knowing the total consumption, the consumption caused by drag, and the drivetrain efficiency, we can estimate the rolling resistance for the Audi e-tron.

Based on driver history, driving on a dry road at 80 km/h in summer requires around 19 kWh/100 km from the battery. Assuming 80% drivetrain efficiency, the total energy need is 15.2 kWh/100 km, including drag.

Subtracting the energy needed for drag, we have around 8.95 kWh/100 km to overcome rolling resistance.

This estimate varies with road conditions; wet or snowy roads increase rolling resistance.

Consumption summary

The diagram below shows the calculated consumption needed to overcome drag and rolling resistance, and the consumption from the battery based on 80% drivetrain efficiency. The actual efficiency is expected to be around 80%.

See the full table with kinetic energy and consumption for all speeds from 1-100 mph (1-161 km/h).

Is regen the best option always?

Since regenerative braking is only 80% efficient, it is best to avoid using it when possible. For scenario 1, driving down Pikes Peak is impossible without regenerative braking. Without regen, you would crash. However, on flat roads in scenarios 2 and 3, it is better to look ahead and let the car coast, using rolling resistance and aerodynamic drag to reduce speed.

This means lifting your foot off the accelerator early enough to stop at the desired point naturally.

How much energy would that save? Two factors reduce total consumption:

• You will not lose 20% of the kinetic energy during regeneration.
• You will not lose 20% of the energy trying to maintain speed.

Theoretically, this can save:

• Scenario 2: 1.89 kWh/100 km
• Scenario 3: 3.02 kWh/100 km

However, this is in the best-case scenario where you can precisely calculate when to lift your foot off the accelerator. In reality, the benefit would be smaller, as you may need to add some power or braking at the end if you miscalculate.

Can you see in the car how much was regenerated?

A common misunderstanding is that you can look at the range reported in the car to see how much was regenerated. For most cars, this is not possible.

The range meter bases its calculation on the last 100 km driven. If we take scenario 4 and assume the car has been driven from sea level up to the top at 650 meters at 80 km/h (49.7 mph), the consumption would be 25.4 kWh/100 km at 650 meters.

For an Audi e-tron 55 with an 86.5 kWh battery capacity, the range would be calculated to 340 km (211 miles) for a full battery based on this consumption.

After driving down the road section in scenario 4, the total consumption from the battery would be reduced from 25.4 kWh/100 km to 21 kWh/100 km.

This would increase the calculated range to 411 km (255 miles) for a fully charged battery (less depending on the real SOC). Based on this, you might mistakenly believe that you have regenerated 71 km (44 miles), but the correct amount is 6.8 km (4.2 miles).

This type of increase can even be seen in scenarios where there is no regeneration, but just a decline that reduces the consumption.

The only way to know how much you have regenerated is to look at how much the state of charge of the battery changes from the top to the bottom of the mountain.

One-pedal driving vs. manual/automatic regen

Depending on the EV, you can use regenerative brakes in different ways:

• Manual: only using the brake pedal
• Automatic: letting the car decide when to regenerate
• One-pedal driving: automatic regeneration when lifting the foot off the accelerator pedal

All methods use the same electric drivetrain components for braking, so they have the same efficiency.

However, one-pedal driving has slightly reduced efficiency in scenarios where the driver wants to transition from using power to coasting.

Since you need to keep your foot on the pedal at a specific position to neither use energy nor brake, you will always spend more time finding this position than simply lifting your foot off the pedal. Additionally, it takes some training to keep the foot in the perfect place.

That’s why manufacturers like Audi, Mercedes, and Porsche recommend using automatic regen with coasting to save energy.

The difference is small, probably less than 10% of the difference between coasting and regenerative braking in scenarios where coasting is possible.

There is no difference for scenarios like scenario 1 since you will use regenerative braking to keep the car on the road.

Since the difference is so small, you should choose based on your preference.